Putting Freebase in a Star Schema
What’s Freebase?

Freebase is a open database of things that exist in the world: things like people, places, songs and television shows. As of the January 2009 dump, Freebase contained about 241 million facts, and it’s growing all the time. You can browse it via the web and even edit it, much like Wikipedia. Freebase also has an API that lets programs add data and make queries using a language called MQL. Freebase is complementary to DBpedia and other sources of information. Although it takes a different approach to the semantic web than systems based on RDF standards, it interoperates with them via linked data.
The January 2009 Freebase dump is about 500 MB in size. Inside a bzip-compressed files, you’ll find something that’s similar in spirit to a Turtle RDF file, but is in a simpler format and represents facts as a collection of four values rather than just three.
Your Own Personal Freebase
To start exploring and extracting from Freebase, I wanted to load the database into a star schema in a mysql database — an architecture similar to some RDF stores, such as ARC. The project took about a week of time on a modern x86 server with 4 cores and 4 GB of RAM and resulted in a 18 GB collection of database files and indexes.
This is sufficient for my immediate purposes, but future versions of Freebase promise to be much larger: this article examines the means that could be used to improve performance and scalability using parallelism as well as improved data structures and algorithms.
I’m interested in using generic databases such as Freebase and Dbpedia as a data source for building web sites. It’s possible to access generic databases through APIs, but there are advantages to having your own copy: you don’t need to worry about API limits and network latency, and you can ask questions that cover the entire universe of discourse.
Many RDF stores use variations of a format known as a Star Schema for representing RDF triples; the Star Schema is commonly used in data warehousing application because it can efficiently represent repetitive data. Freebase is similar to, but not quite an RDF system. Although there are multiple ways of thinking about Freebase, the quarterly dump files provided by Metaweb are presented as quads: groups of four related terms in tab-delimited terms. To have a platform for exploring freebase, I began a project of loading Freebase into a Star Schema in a relational database.
A Disclaimer
Timings reported in this article are approximate. This work was done on a server that was doing other things; little effort was made to control sources of variation such as foreign workload, software configuration and hardware characteristics. I think it’s orders of magnitude that matter here: with much larger data sets becoming available, we need tools that can handle databases 10-100 times as big, and quibbling about 20% here or there isn’t so important. I’ve gotten similar results with the ARC triple store. Some products do about an order of magnitude better: the Virtuoso server can load DBpedia, a larger database, in about 16 to 22 hours on a 16 GB computer: several papers on RDF store performance are available [1] [2] [3]. Although the system described in this paper isn’t quite an RDF store, it’s performance is comprable to a relatively untuned RDF store.
It took about a week of calendar time to load the 241 million quads in the January 2009 Freebase into a Star Schema using a modern 4-core web server with 4GB of RAM; this time could certainly be improved with microoptimizations, but it’s in the same range that people are observing that it takes to load 10^8 triples into other RDF stores. (One product is claimed to load DBPedia, which contains about 100 million triples, in about 16 hours with “heavy-duty hardware”.) Data sets exceeding 10^9 triples are becoming rapidly available — these will soon exceed what can be handled with simple hardware and software and will require new techniques: both the use of parallel computers and optimized data structures.
The Star Schema
In a star schema, data is represented in separate fact and dimension tables,
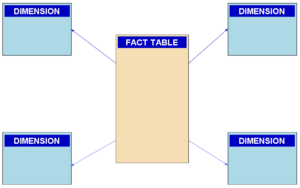
all of the rows in the fact table (quad) contain integer keys — the values associated with the keys are defined in dimension tables (cN_value). This efficiently compresses the data and indexes for the fact table, particularly when the values are highly repetitive.
I loaded data into the following schema:
create table c1_value ( id integer primary key auto_increment, value text, key(value(255)) ) type=myisam; ... identical c2_value, c3_value and c4_value tables ... create table quad ( id integer primary key auto_increment, c1 integer not null, c2 integer not null, c3 integer not null, c4 integer not null ) type=myisam;
Although I later created indexes on c1, c2, c3, and c4 in the quad table, I left unnecessary indexes off of the tables during the loading process because it’s more efficient to create indexes after loading data in a table. The keys on the value fields of the dimension tables are important, because the loading process does frequent queries to see if values already exist in the dimension table. The sequentially assigned id in the quad field isn’t necessary for many applications, but it gives each a fact a unique identity and makes the system aware of the order of facts in the dump file.
The Loading Process
The loading script was written in PHP and used a naive method to build the index incrementally. In pseudo code it looked something like this:
function insert_quad($q1,$q2,$q3,$q4) {
$c1=get_dimension_key(1,$q1);
$c2=get_dimension_key(2,$q2);
$c3=get_dimension_key(3,$q3);
$c4=get_dimension_key(4,$q4);
$conn->insert_row("quad",null,$c1,$c2,$c3,$c4)
}
function get_dimension_key($index,$value) {
$cached_value=check_cache($value);
if ($cached_value)
return $cached_value;
$table="$c{$index}_value";
$row=$conn->fetch_row_by_value($table,$value);
if ($row)
return $row->id;
$conn->insert_row($table,$value);
return $conn->last_insert_id
};
Caching frequently used dimension values improves performance by a factor of five or so, at least in the early stages of loading. A simple cache management algorithm, clearing the cache every 500,000 facts, controls memory use. Timing data shows that a larger cache or better replacement algorithm would make at most an increment improvement in performance. (Unless a complete dimension table index can be held in RAM, in which case all read queries can be eliminated.)
I performed two steps after the initial load:
- Created indexes on quad(c1), quad(c2), quad(c3) and quad(c4)
- Used myisam table compression to reduce database size and improve performance
Loading Performance
It took about 140 hours (nearly 6 days) to do the initial load. Here’s a graph of facts loaded vs elapsed time:
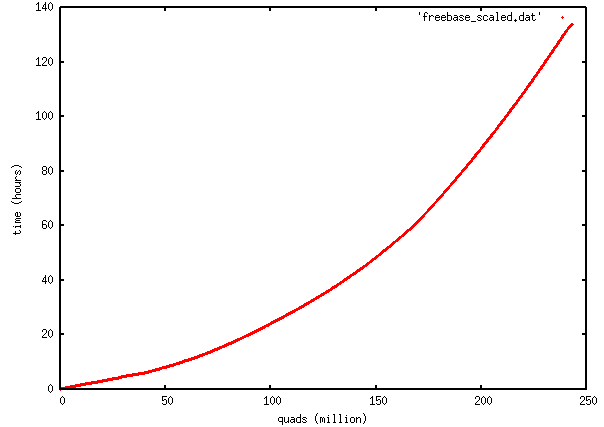
The important thing Iabout this graph is that it’s convex upward: the loading process slows down as the number of facts increases. The first 50 quads are loaded at a rate of about 6 million per hour; the last 50 are loaded at a rate of about 1 million per hour. An explanation of the details of the curve would be complex, but log N search performance of B-tree indexes and the ability of the database to answer queries out of the computer’s RAM cache would be significant. Generically, all databases will perform the same way, becoming progressively slower as the size of the database increases: you’ll eventually reach a database size where the time to load the database becomes unacceptable.
The process of constructing b-tree indexes on the mysql tables took most of a day. On average it took about four hours to construct a b-tree index on one column of quad:
mysql> create index quad_c4 on quad(c4); Query OK, 243098077 rows affected (3 hours 40 min 50.03 sec) Records: 243098077 Duplicates: 0 Warnings: 0
It took about an hour to compress the tables and rebuild indexes, at which point the data directory looks like:
-rw-r----- 1 mysql root 8588 Feb 22 18:42 c1_value.frm -rw-r----- 1 mysql root 713598307 Feb 22 18:48 c1_value.MYD -rw-r----- 1 mysql root 557990912 Feb 24 10:48 c1_value.MYI -rw-r----- 1 mysql root 8588 Feb 22 18:56 c2_value.frm -rw-r----- 1 mysql root 485254 Feb 22 18:46 c2_value.MYD -rw-r----- 1 mysql root 961536 Feb 24 10:48 c2_value.MYI -rw-r----- 1 mysql root 8588 Feb 22 18:56 c3_value.frm -rw-r----- 1 mysql root 472636380 Feb 22 18:51 c3_value.MYD -rw-r----- 1 mysql root 370497536 Feb 24 10:51 c3_value.MYI -rw-r----- 1 mysql root 8588 Feb 22 18:56 c4_value.frm -rw-r----- 1 mysql root 1365899624 Feb 22 18:44 c4_value.MYD -rw-r----- 1 mysql root 1849223168 Feb 24 11:01 c4_value.MYI -rw-r----- 1 mysql root 65 Feb 22 18:42 db.opt -rw-rw---- 1 mysql mysql 8660 Feb 23 17:16 quad.frm -rw-rw---- 1 mysql mysql 3378855902 Feb 23 20:08 quad.MYD -rw-rw---- 1 mysql mysql 9927788544 Feb 24 11:42 quad.MYI
At this point it’s clear that the indexes are larger than the actual databases: note that c2_value is much smaller than the other tables because it holds a relatively small number of predicate types:
mysql> select count(*) from c2_value; +----------+ | count(*) | +----------+ | 14771 | +----------+ 1 row in set (0.04 sec) mysql> select * from c2_value limit 10; +----+-------------------------------------------------------+ | id | value | +----+-------------------------------------------------------+ | 1 | /type/type/expected_by | | 2 | reverse_of:/community/discussion_thread/topic | | 3 | reverse_of:/freebase/user_profile/watched_discussions | | 4 | reverse_of:/freebase/type_hints/included_types | | 5 | /type/object/name | | 6 | /freebase/documented_object/tip | | 7 | /type/type/default_property | | 8 | /type/type/extends | | 9 | /type/type/domain | | 10 | /type/object/type | +----+-------------------------------------------------------+ 10 rows in set (0.00 sec)
The total size of the mysql tablespace comes to about 18GB, anexpansion of about 40 times relative to the bzip2 compressed dump file.
Query Performance
After all of this trouble, how does it perform? Not too bad if we’re asking a simple question, such as pulling up the facts associated with a particular object
mysql> select * from quad where c1=34493; +---------+-------+------+---------+--------+ | id | c1 | c2 | c3 | c4 | +---------+-------+------+---------+--------+ | 2125876 | 34493 | 11 | 69 | 148106 | | 2125877 | 34493 | 12 | 1821399 | 1 | | 2125878 | 34493 | 13 | 1176303 | 148107 | | 2125879 | 34493 | 1577 | 69 | 148108 | | 2125880 | 34493 | 13 | 1176301 | 148109 | | 2125881 | 34493 | 10 | 1713782 | 1 | | 2125882 | 34493 | 5 | 1174826 | 148110 | | 2125883 | 34493 | 1369 | 1826183 | 1 | | 2125884 | 34493 | 1578 | 1826184 | 1 | | 2125885 | 34493 | 5 | 66 | 148110 | | 2125886 | 34493 | 1579 | 1826185 | 1 | +---------+-------+------+---------+--------+ 11 rows in set (0.05 sec)
Certain sorts of aggregate queries are reasonably efficient, if you don’t need to do them too often: we can look up the most common 20 predicates in about a minute:
select
(select value from c2_value as v where v.id=q.c2) as predicate,count(*)
from quad as q
group by c2
order by count(*) desc
limit 20;
+-----------------------------------------+----------+ | predicate | count(*) | +-----------------------------------------+----------+ | /type/object/type | 27911090 | | /type/type/instance | 27911090 | | /type/object/key | 23540311 | | /type/object/timestamp | 19462011 | | /type/object/creator | 19462011 | | /type/permission/controls | 19462010 | | /type/object/name | 14200072 | | master:9202a8c04000641f800000000000012e | 5541319 | | master:9202a8c04000641f800000000000012b | 4732113 | | /music/release/track | 4260825 | | reverse_of:/music/release/track | 4260825 | | /music/track/length | 4104120 | | /music/album/track | 4056938 | | /music/track/album | 4056938 | | /common/document/source_uri | 3411482 | | /common/topic/article | 3369110 | | reverse_of:/common/topic/article | 3369110 | | /type/content/blob_id | 1174046 | | /type/content/media_type | 1174044 | | reverse_of:/type/content/media_type | 1174044 | +-----------------------------------------+----------+ 20 rows in set (43.47 sec)
You’ve got to be careful how you write your queries: the above query with the subselect is efficient, but I found it took 5 hours to run when I joined c2_value with quad and grouped on value. A person who wishes to do frequent aggregate queries would find it most efficient to create a materialized views of the aggregates.
Faster And Large
It’s obvious that the Jan 2009 Freebase is pretty big to handle with the techniques I’m using. One thing I’m sure of is that that Freebase will be much bigger next quarter — I’m not going to do it the same way again. What can I do to speed the process up?
Don’t Screw Up
This kind of process involves a number of lengthy steps. Mistakes, particularly if repeated, can waste days or weeks. Although services such as EC2 are a good way to provision servers to do this kind of work, the use of automation and careful procedures is key to saving time and money.
Partition it
Remember how the loading rate of a data set decreases as the size of the set increase? If I could split the data set into 5 partitions of 50 M quads each, I could increase the loading rate by a factor of 3 or so. If I can build those 5 partitions in parallel (which is trivial), I can reduce wallclock time by a factor of 15.
Eliminate Random Access I/O
This loading process is slow because of the involvement of random access disk I/O. All of Freebase canbe loaded into mysql with the following statement,
LOAD DATA INFILE ‘/tmp/freebase.dat’ INTO TABLE q FIELDS TERMINATED BY ‘\t’;
which took me about 40 minutes to run. Processes that do a “full table scan” on the raw Freebase table with a grep or awk-type pipeline take about 20-30 minutes to complete. Dimension tables can be built quickly if they can be indexed by a RAM hasthable. The process that builds the dimension table can emit a list of key values for the associated quads: this output can be sequentially merged to produce the fact table.
Bottle It
Once a data source has been loaded into a database, a physical copy of the database can be made and copied to another machine. Copies can be made in the fraction of the time that it takes to construct the database. A good example is the Amazon EC2 AMI that contains a preinstalled and preloaded Virtuoso database loaded with billions of triples from DBPedia, MusicBrainz, NeuroCommons and a number of other databases. Although the process of creating the image is complex, a new instance can be provisioned in 1.5 hours at the click of a button.
Compress Data Values
Unique object identifiers in freebase are coded in an inefficient ASCII representation:
mysql> select * from c1_value limit 10; +----+----------------------------------------+ | id | value | +----+----------------------------------------+ | 1 | /guid/9202a8c04000641f800000000000003b | | 2 | /guid/9202a8c04000641f80000000000000ba | | 3 | /guid/9202a8c04000641f8000000000000528 | | 4 | /guid/9202a8c04000641f8000000000000836 | | 5 | /guid/9202a8c04000641f8000000000000df3 | | 6 | /guid/9202a8c04000641f800000000000116f | | 7 | /guid/9202a8c04000641f8000000000001207 | | 8 | /guid/9202a8c04000641f80000000000015f0 | | 9 | /guid/9202a8c04000641f80000000000017dc | | 10 | /guid/9202a8c04000641f80000000000018a2 | +----+----------------------------------------+ 10 rows in set (0.00 sec)
These are 38 bytes apiece. The hexadecimal part of the guid could be represented in 16 bytes in a binary format, and it appears that about half of the guid is a constant prefix that could be further excised.
A similar efficiency can be gained in the construction of in-memory dimension tables: md5 or sha1 hashes could be used as proxies for values.
The freebase dump is littered with “reverse_of:” properties which are superfluous if the correct index structures exist to do forward and backward searches.
Parallelize it
Loading can be parallelized in many ways: for instance, the four dimension tables can be built in parallel. Dimension tables can also be built by a sorting process that can be performed on a computer cluster using map/reduce techniques. A cluster of computers can also store a knowledge base in RAM, trading sequential disk I/O for communication costs. Since the availability of data is going to grow faster than the speed of storage systems, parallelism is going to become essential for handling large knowledge bases — an issue identified by Japanese AI workers in the early 1980′s.
Cube it?
Some queries benefit from indexes built on combinations of tables, such as
CREATE INDEX quad_c1_c2 ON quad(c1,c2);
there are 40 combinations of columns on which an index could be useful — however, the cost in time and storage involved in creating those indexes would be excessively expensive. If such indexes were indeed necessary, a Multidimensional database can create a cube index that is less expensive than a complete set of B-tree indexes.
Break it up into separate tables?
It might be anathema to many semweb enthusiasts, but I think that Freebase (and parts of Freebase) could be efficiently mapped to conventional relational tables. That’s because facts in Freebase are associated with types, see, for instance, Composer from the Music Commons. It seems reasonable to map types to relational tables and to create satellite tables to represent many-to-many relationships between types. This scheme would automatically partition Freebase in a reasonable way and provide an efficient representation where many obvious questions (ex. “Find Female Composers Born In 1963 Who Are More Than 65 inches tall”) can be answered with a minimum number of joins.
Conclusion
Large knowledge bases are becoming available that cover large areas of human concern: we’re finding many applications for them. It’s possible to to handle databases such as Freebase and DBpedia on a single computer of moderate size, however, the size of generic databases and the hardware to store them on are going to grow larger than the ability of a singler computer to process them. Fact stores that (i) use efficient data structures, (ii) take advantage of parallelism, and (iii) can be tuned to the requirements of particular applications, are going to be essential for further progress in the Semantic Web.
Credits
- Metaweb Technologies, Freebase Data Dumps, January 13, 2009
- Kingsley Idehen, for several links about RDF store performance.
- Stewart Butterfield for encyclopedia photo.
Paul Houle on February 25th 2009 in Freebase, SQL, Semantic Web
![[Generation Five]](/q/wp-content/themes/mach-go/images/GenerationFive.png)
![[Reliable And Maintainable Software For The Next Generation]](/q/wp-content/themes/mach-go/images/ReliableAndMaintainableSoftwareForTheNextGeneration.png)

